⊂Xn = Y , such that Xi is a primitive multiple scheme of multiplicity i. The
ideal sheaf ℐX of X is a line bundle on Xn−1 and L = ℐX∕ℐX2 is a line bundle on X, called the
associated line bundle of Y .
A primitive multiple scheme is a Cohen-Macaulay scheme Y such that the associated reduced
scheme X = Y red is smooth, irreducible, and that Y can be locally embedded in a smooth
variety of dimension dim(X) + 1. If n is the multiplicity of Y , there is a canonical filtration
X = X1 ⊂X2 ⊂⊂Xn = Y , such that Xi is a primitive multiple scheme of multiplicity i. The
ideal sheaf ℐX of X is a line bundle on Xn−1 and L = ℐX∕ℐX2 is a line bundle on X, called the
associated line bundle of Y .
Even if X is projective, Y needs not to be quasi projective. We define in every case the reduced Hilbert polynomial Pred,𝒪X(1)(E) of a coherent sheaf E on Y , depending on the choice of an ample line bundle 𝒪X(1) on X. If ℰ is a flat family of sheaves on Y parameterized by a smooth curve C, then Pred,𝒪X(1)(ℰc) does not depend on c ∈C. We study flat families of sheaves in two important cases: the families of quasi locally free sheaves, and if n = 2 those of balanced sheaves. Balanced sheaves are generalizations of vector bundles on Y , and could be used to expand already known moduli spaces of vector bundles on Y .
When X is a smooth projective surface, and Y is of multiplicity 2 we study the simplest examples of balanced sheaves: the sheaves ℰ such that there is an exact sequence
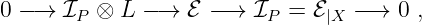
where ℐP ⊂𝒪X is the ideal sheaf of a point P ∈X. They can also be described as the ideal sheaves ℰ of subschemes of Y concentrated on P, and such that ℰP is generated by two elements whose images in 𝒪X,P generate the maximal ideal. There is a moduli space for such sheaves, which is an affine bundle on X with associated vector bundle TX ⊗L (where TX is the tangent bundle of X). The associated class in H1(X,T X ⊗L) can be determined.