



Next: Bessel transforms
Up: Theoretical background
Previous: Functions
Contents
Index
Fourier transforms
Let 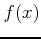 be a real or complex function defined on the interval
be a real or complex function defined on the interval ![$[0,L]$](img8.gif) . Let
. Let
be the Fourier transform of 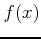 . Let
. Let 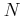 a power of
a power of 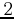 , and
, and
The discrete Fourier transform of 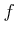 is
is
It is the true Fourier transform of the function
which is an approximation of 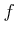 . Here we assume that
. Here we assume that 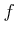 is linear between
is linear between
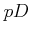 and
and 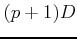 , hence we have the exact formula
, hence we have the exact formula
A FFT would give the value of 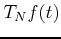 for all multiples of
for all multiples of 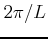 .
Suppose we have
.
Suppose we have
with 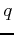 an integer and
an integer and
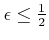 . Then we have
. Then we have
Developping the last exponential, we get
This means that we would get the exact formula for 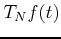 if we had all
the FFT's of the functions
if we had all
the FFT's of the functions
In fact only the 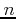 between 0 and 20 are needed to get double precision. We
can even reduce this number by taking approximations of the exponential
using Tschebychev polynomials.
between 0 and 20 are needed to get double precision. We
can even reduce this number by taking approximations of the exponential
using Tschebychev polynomials.
We can of course also define Fourier transforms of a function 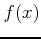 defined
on an arbitrary interval
defined
on an arbitrary interval ![$[a,b]$](img28.gif) , by first computing the Fourier transform of
, by first computing the Fourier transform of
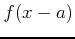 (defined on
(defined on ![$[0,b-a]$](img30.gif) ) and multiplying the result by
) and multiplying the result by 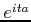 .
.




Next: Bessel transforms
Up: Theoretical background
Previous: Functions
Contents
Index
2009-11-12
![]() be a real or complex function defined on the interval
be a real or complex function defined on the interval ![]() . Let
. Let
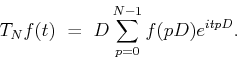
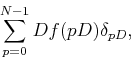
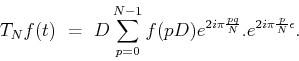
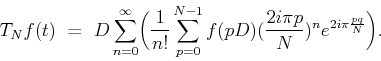
![]() defined
on an arbitrary interval
defined
on an arbitrary interval ![]() , by first computing the Fourier transform of
, by first computing the Fourier transform of
![]() (defined on
(defined on ![]() ) and multiplying the result by
) and multiplying the result by ![]() .
.