



Next: Plane geometry
Up: Theoretical background
Previous: Fourier transforms
Contents
Index
Bessel transforms
Let 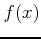 a real function defined on an interval
a real function defined on an interval ![$[a,b]$](img28.gif) ,
, 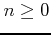 an
integer. The
an
integer. The 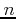 -th Bessel transform of
-th Bessel transform of 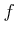 is the function
is the function
where 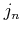 is the Bessel function of order
is the Bessel function of order 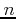 . Let
. Let 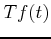 the Fourier
transform of
the Fourier
transform of 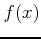 and
and 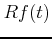 ,
, 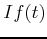 the real and imaginary part of
the real and imaginary part of
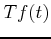 :
:
Then we have
We use these formulas to compute Bessel transforms in funct.
2009-11-12
![]() a real function defined on an interval
a real function defined on an interval ![]() ,
, ![]() an
integer. The
an
integer. The ![]() -th Bessel transform of
-th Bessel transform of ![]() is the function
is the function