Le 05 mai
 

-Alan T. Huckleberry- (Bochum)
-Asymptotic equivariant index and Atiyah Weintein conjecture.
_{A flag domain is an open orbit D of a noncompact real semisimple Lie group G0 in a flag manifold Z=G/Q of its complexification G. These appear naturally in representation theoretical and complex analytic contexts. In most cases D possesses no nonconstant holomorphic functions, but nevertheless has infinite-dimensional Dolbeault cohomology in a certain expected dimension. A large part of this cohomology can be transferred to the level of holomorphic functions on an associated Barlet cycle space C}^q_{(D). Recently it was shown that these cycle spaces vary dramatically as D varies as an open orbit in Z and as Z varies as a G-flag manifold, and therefore provide a wide range of complex spaces with G0-symmetry. In the lecture we will outline background, sketch several examples and outline the proof of the fact that these cycle spaces are Kobayashi hyperbolic Stein spaces..}

Le 12 mai
 

-Duong Hong Phong- (Columbia)
-The Dirichlet problem for Monge-Ampère equations on Kähler manifolds.
A survey is presented of methods for solving the Dirichlet problem for Monge-Ampère equations on K\"ahler manifolds with boundary, including pluripotential theory and a priori estimates. Emphasis will be on the degenerate case, and especially on the construction of geodesic rays in the space of Kähler metrics, which plays a central role in Donaldson's notion of infinite-dimensional geometric invariant theory.

Le 19 mai
 

-Charles Epstein- (Pennsylvania)
-Numerical solution of Maxwell's equations.

Le 26 mai
 

-Claudio Arezzo- (Parma)
-Complexi ed Kähler-Ricci ow on families of complex manifolds.
We present a joint work with La Nave on the convergence properties of the Kähler-Ricci ow on manifolds with positive forst Chern class. Based on the symplectic reduction construction of La Nave-Tian, we find a static Monge-Ampère equation on the total space of a line bundle over a family of complex manifolds which induces via restriction and reduction on each memebr of the family the Kähler-Ricci flow. By solving this equation for some initial data, we prove a number of convergence results in the case of arbitrary deformations and test configurations.

Le 07 avril
 

-Louis Boutet de Monvel- (IMJ)
-Asymptotic equivariant index and Atiyah Weintein conjecture.
_{In 1974 M.F. Atiyah developed the theory of the equivariant index of transversally elliptic pseudodifferential operators on manifolds with a compact group action. The asymptotic index is an avatar of this theory, which works for equivariant Toeplitz operators (as defined in my book with V. Guillemin). If Y1, Y2 are two complex strictly pseudoconvex domains with boundaries X1, X2 and u a contact isomorphism from X1 to X2, the transport map f→S2(f◦ u}^(-1)_{) from holomorphic functions on X1 to those on X2 has an index (S2 is the Szegö projecteur on X2). An index formula was proposed by A. Weinstein, following a similar formula for Fourier integral operators proposed by Atihah. This index formula was proved by C. Epstein; with E. Leichtnam, X. Tang and A. Weinstein we gave a new "natural" proof using this asymptotic equivariant index theory..}

Le 28 avril
 

A 14h00 -Simone Diverio- (Rome)
-La conjecture de Kobayashi en dimension trois.
La conjecture de Kobayashi prédit que toute hypersurface projective générique de degré assez grand est hyperbolique. On donnera une confirmation de cette conjecture en dimension trois, obtenue récemment en collaboration avec S. Trapani. Pour celle-ci, on discutera une légère amélioration d'un résultat plus général de dégénéressance algébrique des courbes entières obtenu en collaboration avec J. Merker et E. Rousseau..

A 15:00 -Christian Miebach- (Marseille)
-Quotients des domaines bornés\break homogènes par le groupe ${\bf Z}$.
_{Il est connu que le quotient de la boule unité dans C}ⁿ _{par une action holomorphe et propre du groupe Z est une variété de Stein. Nous allons donner une nouvelle preuve de ce fait, puis nous la généraliserons \`a une action holomorphe et propre de Z sur un domaine borné et homogène quelconque. Cela démontre que le quotient d'un domaine borné et homogène par le groupe Z est de Stein.}

Le 03 mars

-Lionel Mason- (Oxford-IHES)
-Einstein-Weyl spaces, scattering maps and holomorphic discs.

Le 10 mars

-Ken-Ichi Yoshikawa- (Tokyo)
-Analytic torsion for certain Calabi-Yau threefolds.
In this talk, I explain the construction of an invariant of Calabi-Yau threefold, the "BCOV invariant", which we obtain using analytic torsion. I give some examples of Calabi-Yau threefolds whose BCOV invariant is explicitly determined as a function on the moduli space. If time permits, I explain the physics conjecture about the structure of the BCOV invariant. Large part of this talk is based on the joint work with Hao Fang and Zhiqin Lu..

Le 17 mars
 

-Gilles Courtois- (Ecole polytechnique de Paris)
-Théorème d'annulation homologique en courbure négative.
_{Soit G un groupe discret d'isométries d'une variété X simplement connexe de courbure négative. Pour un entier k supérieur ou égal à deux, l'homologie réelle de X/G s'annule lorsque la dimension de Hausdorff de l'ensemble limite de G est inférieure à k-1. Nous établirons un lien entre ce genre de théorème d'annulation et la conjecture de Lehmer.}

Le 24 mars
Exposé annulé
pour cause de manifestation

-Matei Toma- (Nancy)
-Fibrations rationnellement connexes et stabilité du fibré tangent.
_{Les termes de la filtration de Harder-Narasimhan du fibré tangent d'une variété projective lisse induisent une suite de fibrations de cette variété à fibres rationnellement connexes. Alors que la filtration de Harder-Narasimhan dépend de la polarisation par rapport à laquelle on a considéré la notion de stabilité, il existe une fibration rationnellement connexe maximale de la variété. On montre qu'il existe une "polarisation" qui permet de retrouver cette fibration rationnellement connexe maximale par la correspondance ci-dessus. Pour le faire, on considére des polarisations qui correspondent aux courbes mobiles de la variété et qui sont plus générales que les polarisations amples usuelles. Une difficulté de cette approche est l'absence d'un théorème de restriction de type Mehta-Ramanathan dans ce cas.}

Le 31 mars
 

A 15:00 -Matei Toma- (Nancy)
-Fibrations rationnellement connexes et stabilité du fibré tangent.
_{Les termes de la filtration de Harder-Narasimhan du fibré tangent d'une variété projective lisse induisent une suite de fibrations de cette variété à fibres rationnellement connexes. Alors que la filtration de Harder-Narasimhan dépend de la polarisation par rapport à laquelle on a considéré la notion de stabilité, il existe une fibration rationnellement connexe maximale de la variété. On montre qu'il existe une "polarisation" qui permet de retrouver cette fibration rationnellement connexe maximale par la correspondance ci-dessus. Pour le faire, on considére des polarisations qui correspondent aux courbes mobiles de la variété et qui sont plus générales que les polarisations amples usuelles. Une difficulté de cette approche est l'absence d'un théorème de restriction de type Mehta-Ramanathan dans ce cas.}

Le 03 février

Antonin Guilloux (ENS-Lyon)
-Autour des orbites d’un réseau dans le plan.
_{La distribution des orbites d’un point du plan sous l’action des matrices de SL(2,Z) peut-être vue comme une manifestation concrète d’un phénomène de rigidité pour un problème dual : la distribution des orbites du groupe unipotent dans le quotient SL(2,R)/SL(2,Z). Le théorème de Ratner et ses avatars sont des outils puissants pour étudier ce deuxième problème ; en particulier, Ledrappier a expliqué comment les utiliser pour décrire les orbites dans le plan.  A partir de la présentation de ces idées, j’exposerai des généralisations possibles dans d’autres espaces homogènes (avec en tête des applications arithmétiques), ainsi que des liens possibles avec
l’approximation diophantienne.}

Le 10 février

Ma Xioanan (IMJ)
Quantification géométrique pour les applications moment propres.
Nous établissons une formule de quantification géométrique pour les actions hamiltoniennes d’un groupe de Lie compact agissant sur une variété symplectique non-compacte dont l’application moment est propre. En particulier, nous résolvons une conjecture formulée par Michèle Vergne dans son exposé plénier `a l’ICM 2006.

Le 17 février
 

Daniel Burns (Michigan)
Variétés toriques et la correspondance de Bohr-Sommerfeld.
_{On espère, dans la théorie de la quantification géométrique, que les quantifications produites en suivant deux fa¸cons de quantification (par exemple, en utilisant deux polarisations distinctes) doivent être isomorphes, de préférence par une équivalence canonique. Nous considérons cette correspondance dans le cas, d’abord, d’une variété torique X de dimension complexe n, polarisée, dans le sens de la géométrie algébrique, par un fibré en droites L, en la quantifiant par la polarisation réelle induite par l’action du tore réel Tn, et par la polarisation complexe induite par L. La correspondance cherchée est la correspondance classique de Bohr-Sommerfeld, et c’est assez facile dans ce cas. On procède aux cas des variétés toriques singulières, dans plusieurs sens. Un rôle clé est joué par les déformations de variétés algébriques, et en particulier, les dégénérescences toriques de variétés. Cette approche débouche sur des problèmes intéressants toujours ouverts. Les résultats nouveaux ici sont produits d’un ensemble de collaborations avec Victor Guillemin, Alejandro Uribe et Zuoqin Wang. Quelques idées qui apparaissent ici remontent en partie `a Andrei Tyurin..}

Le 24 février
 

Serguei Ivachkovitch (Lille)
Cycles évanouissants dans les feuilletages holomorphes par des courbes complexes et les «coquilles feuilletées».
_{Les cycles évanouissants introduit par S. P Novikov pour les feuilletages de codimension 1 jouent en fait un rô1e essentiel dans la description des feuilletages en toute codimension. On espère que l’existence d’un cycle évanouissant dans une feuille d’un feuilletage par surfaces entraîne la compacité de cette même feuille qui le porte. Nous allons étudier les feuilletages holomorphes par courbes complexes dans les variétés complexes compactes. Le résultat principal de notre exposé consiste de démontrer que la présence d’un cycle évanouissant est équivalent `a la présence d un objet beaucoup plus riche d’une “coquille feuilletée”..}

Le 06 janvier

Elisha Falbel (IMJ)
Triangulations des variétés CR.
_{Je discuterai les triangulations des variétés de Cauchy-Riemann de dimension trois et leurs invariants combinatoires.}

Le 13 janvier

Dan Popovici (Toulouse)
Limites de variétés projectives par déformations holomorphes.
Si toutes les fibres, sauf une, d'une famille analytique complexe de variétés complexes compactes lisses sont supposées projectives, on essayera de montrer que la fibre limite doit être de Moishezon.

Le 20 janvier
 

Joël Fine (Bruxelles)
Calabi flow and projective embeddings.
_{The Calabi flow is a natural parabolic flow which attempts to deform a Kähler metric until it has constant scalar curvature. I will explain how this flow can be seen as the "classical limit" of a flow in projective geometry called balancing flow. Given a smooth subvariety X of CP}^N_{, balancing flow deforms the given embedding through projectively equivalent embeddings until it is "balanced" (a notion I will define in the talk and which Donaldson has shown is the quantisation of "constant scalar curvature"). Tian has explained how to find a sequence of embeddings into successively larger projective spaces such that the restriction of the Fubini-Study metric converges to a given Kähler metric. Running balancing flow on each of these embeddings and pulling back the Fubini-Study metric gives a sequence of metric flows which converge to the Calabi flow starting at the given Kähler metric for as long as the flow exists.}

Le 27 janvier
 

Erwan Rousseau (Strasbourg)
Sur la conjecture de Green-Griffiths.
_{La conjecture de Green-Griffiths stipule que dans toute variété projective de type général il existe une sous-variété propre qui contient toutes les courbes entières non-constantes. J'exposerai quelques résultats qui confirment cette conjecture dans différents contextes. Avec S. Diverio et J. Merker, nous avons obtenu une preuve de cette conjecture pour les hypersurfaces, génériques de grands degrés (effectifs) de l'espace projectif. J'ai étudié une généralisation de cette conjecture au contexte orbifolde (au sens de F. Campana) et présenterai les résultats obtenus et leurs applications dans le cas des surfaces orbifoldes.}

Le 02 décembre

Xiuxiong Chen (Madison)
A simple lemma in calculus and its application in Kähler geometry.

Le 09 décembre
 

Julien Duval (Orsay)
Sur le deuxième théorème de Nevanlinna.
Le deuxième théorème de Nevanlinna mesure l’impact d’une courbe entière sur des cibles fixes dans la sphère de Riemann. J’exposerai sa généralisation (due à Yamanoi) aux cibles mobiles..

Le 16 décembre
 

Gennadi Henkin (IMJ)
Formules de type Cauchy-Pompeiu sur les surfaces de Riemann et problème de conductivité inverse .
_{Nous avons obtenu (Henkin, arXiv:0804.3761.2008) les versions explicites et des expressions pour la décomposition de Hodge-Riemann sur les surfaces de Riemann. L’une des applications est la solution du problème de reconstitution effective de tenseur de conductivité d’une surface X à bord dans R}³ _{à partir des mesures électriques sur la frontière de X. Cette application généralise les résultats originaux de R. Novikov (1988) et de J. Sylvester (1990), obtenus pour les surfaces simplement connexes. Le cas de conductivité isotrope est obtenu dans G. Henkin et V. Michel, J. Geom. Anal. 2008.}

Le 04 novembre

10:00 salle 0D1 : Joël Merker (ENS Paris)
Application de la théorie effective des invariants à l'hyperbolicité au sens de Kobayashi, et à la dégénérescence algébrique au sens de Green-Griffiths

A 11h15 salle 0D1 : Jean-Pierre Demailly (Grenoble)
Métriques hermitiennes pseudo-effectives et volume des classes de type (1,1)

A 14:00 salle 7D1 : Thomas Peternell(Bayreuth)
Ample subvarieties and a conjecture of Hartshorne.

Le 18 novembre
 

Mihai Paun (Nancy)
Noyaux de Bergman et Non-Annulation.
Je vais essayer de motiver et commenter quelques résultats récents, dont certains ont été obtenus en collaboration avec Bo Berndtsson.

Le 25 novembre
 

Richard Wentworth (University of Maryland)
The Yang-Mills flow on Kähler surfaces .
_{We will explain the behavior of the Yang-Mills flow of integrable connections on hermitian complex vector bundles over Kaehler surfaces. In particular, we will show that flow converges, in an appropriate sense which takes into account bubbling phenomena, to the double dual of the graded sheaf associated to the Harder-Narasimhan-Seshadri filtration of the initial holomorphic bundle. This generalizes to Kaehler surfaces the known result on Riemann surfaces and proves, in this case, a conjecture of Bando and Siu.}

Le 07 octobre

Sorin Dumitrescu (Orsay)
Connexions affines et projectives sur les surfaces complexes compactes.
_{Soit (S,D) une surface complexe compacte connexe munie d'une connexion affine holomorphe sans torsion D. Nous démontrons que D est localement modelée sur une connexion affine invariante par translations sur C² (en particulier, D est localement homogène), sauf si S est un fibré elliptique principal au-dessus d'une surface de genre au moins 2, de premier nombre de Betti impair et D est une connexion affine holomorphe sans torsion générique sur D, auquel cas l'algèbre de Lie des champs de Killing locaux est de dimension un, engendrée par le champ fondamental de la fibration principale. Nous en déduisons que toute connexion projective holomorphe normale sur une surface complexe compacte est plate.}

Le 14 octobre
 

Fedor Pakovich (Beer-Sheva, Israel)
On the polynomial moment problem.
Abstract. About ten years ago in the series of papers of M. Briskin, J.-P. Francoise and Y. Yomdin the following problem arose: "for a given complex polynomial P and complex numbers a,b to describe polynomials q orthogonal to all powers of P on the segment [a,b]". Posed initially as an intermediate step of a broad research program concerning Poincare center-focus problem, the polynomial moment problem turned out to be quite subtle question unexpectedly related to such branches of mathematics as Galois theory, Representation Theory, and Combinatorics. In the talk we outline the recent solution of the polynomial moment problem obtained by F.Pakovich and M. Muzychuk and discuss different applications and generalizations. .

Le 21 octobre
 

A 14:00
Vyacheslav Zakharyuta (Sabanci University)
Kolmogorov problem on widths asymptotic.
_{Given a compact set in an open set on a Stein manifold the set of all restrictions of functions, analytic in with absolute value bounded by is considered as a compact subset in . The problem about the strict asymptotics for Kolmogorov diameters: was stated by Kolmogorov (in an equivalent formulation for -entropy of this set). It was conjectured in [1,2] that for "good" pairs the asymptotics (1) holds with , where is the pluricapacity of the "pluricondenser" inroduced by Bedford and Taylor. In the one-dimensional case this hypothesis is equivalent to Kolmogorov's conjecture about asymptotics of -entropy of the set which has been confirmed by efforts of many authors (Erokhin, Babenko, Zahariuta, Levin-Tikhomirov, Widom, Nguyen, Skiba - Zahariuta, Fisher - Miccheli, et al.}

_{In [1,2] (the detailed proof is in [3]) it was shown that the problem (1) can be reduced to the problem of Pluripotential Theory about approximation of Green pluripotential of the pluricondenser by pluripotentials with finite set of logarithmic singularities. In our talk we discuss a final solution of the Kolmogorov problem, which is a synthesis of our results about this reduction and the recent result of Nivoche and Poletsky, solving above problem on approximation of Green pluripotential. Some related unsolved problem will be discussed.}

_{[1] Zahariuta, V., Spaces of analytic function and maximal plurisubharmonic functions, Dr. Sci. Thesis, Rostov State University, Rostov-na-Donu, 1984, 281pp.}

_{[2] V. Zahariuta, Spaces of analytic function and complex potential theory, in: Linear Topological Spaces and Complex Analysis 1 (1994), 74-146.}

_{[3] V. Zahariuta, Kolmogorov problem on widths asymptotics and pluripotential theory, Proceedings of Conference in Functional Analysis and Complex Analysis (Istanbul, 17-21 September, 2007), Contemporary Mathematics, to appear.}

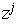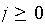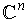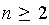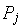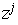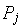Classical Fourier analysis in the unit disk is based on the characters , . Fourier analysis in the unit ball of , , uses Ryll-Wojtaszczyk polynomials in the place of . By definition, is a holomorphic homogeneous polynomial of degree 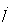and the 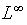and 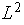norms of 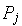are uniformly comparable for all integers j.

_{We discuss results of the Fourier analysis in the unit ball; in particular, we consider the following questions:}

_{1. Examples of Bloch functions with no radial limits (D. Ullrich). Examples of highly non-integrable holomorphic functions in the ball (J. Globevnik, P. Jakóbczak and P. Wojtaszczyk).}

_{2. Zygmund's dichotomy for pluriharmonic Riesz products. This dichotomy yields examples of bounded holomorphic functions with special properties; in particular, we consider weakly outer inner functions and inner functions in the little Bloch space.}

_{3. A characterization of the Bloch-to-BMOA composition operators in the ball (O. Blasco, M. Lindström and J. Taskinen). A description of the radial Bloch--Carleson measures. Characterizations of the bounded and compact weighted composition operators from a growth space to a Bergman space in the ball.}

Le 28 octobre
 

Christophe Mourougane (Rennes)
Métriques de Hodge sur des images directes supérieures.
_{La théorie de variations de structures de Hodge permet de déterminer la courbure de fibrés vectoriels holomorphes hermitiens, obtenus en mettant en famille des groupes de cohomologie de Dolbeault à coefficients complexes. J’expliquerai comment généraliser ces propriétés de courbure à des fibrés obtenus en mettant en famille des groupes de cohomologie `a coefficients dans des fibrés vectoriels holomorphes semi-positifs. J’expliquerai, en particulier, des techniques de transfert de positivité par image directe, pour des morphismes non nécessairement lisses. C’est un travail en commun avec Shigeharu Takayama.}

Le 23 septembre

Claire Voisin (IHES)
.
Le but de cet exposé est de formuler et surtout motiver la conjecture suivante sur les cônes effectifs : la classe d'une sous-variété «très mobile» est dans l'intérieur du cône effectif. On montrera comment cette conjecture entraîne la conjecture de Hodge-Grothendieck généralisée pour les intersections complètes de coniveau 2..

Le 30 septembre
 

Oscar Garcia-Prada (Madrid)
Higgs bundles and representations of surface groups.
We introduce the theory of G-Higgs bundles over a compact Riemann surface X for any real semisimple Lie group G and show their relation to the representations of the fundamental group of X. We then focus on the case in which G is the isometry group of a non-compact Hermitian symmetric space.